


TSD-SOFT COMPANY
The main objectives of the analysis and assignment
Software development
The most important task in the analysis of experimental data in solid state physics are usually the following tasks:
- formalizability multi-phase Rietveld analysis (primarily for RTOF spectra - the method of time-of-flight).
- definition of the symmetry structure of the powder (Match Powder)
- automatic three-dimensional Fourier synthesis
- indexing multiphase powders
- fit one - and two-dimensional peaks
- different types of filtering data, mathematical statistics, etc.
- formalizability multi-phase Rietveld analysis (primarily for RTOF spectra - the method of time-of-flight).
- definition of the symmetry structure of the powder (Match Powder)
- automatic three-dimensional Fourier synthesis
- indexing multiphase powders
- fit one - and two-dimensional peaks
- different types of filtering data, mathematical statistics, etc.



In nuclear physics the main tasks, as a rule, it is the processing of spectra obtained on different spectrometers, identification of radionuclides by their characteristic peaks and the determination of specific activities of the preparations. An important objective is the correct calibration available spectrometric device and characteristic known elements (calibration samples), peaks are usually easily detected in the spectrum of the calibration. In gamma-ray spectrometry for these purposes usually are used the radionuclides Co-60 and Cs-137.

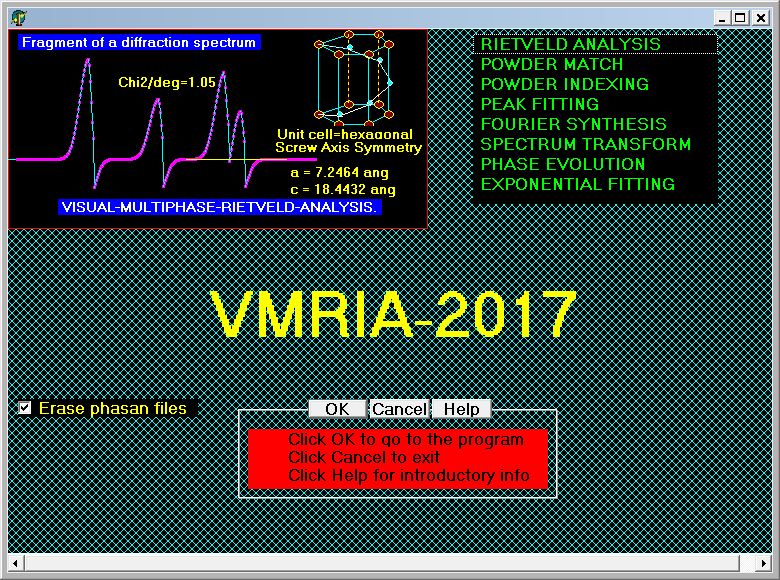
The program VMRIA (Visual Multiphase RIetveld Analysis) focused on a wide class of neutron diffraction data from multiphase polycrystals, as time-of-flight and angular; both direct and Fourier (Reversed Time of Flight) and is open to all sorts of modifications and extensions; the ability to analyze multiple spectra simultaneously multiphase structures (for example, measured at different angles); independent of the peak shape and can work with a regular shape (Gaussian, Lorentzian, etc.), and the most exotic, given, if necessary, graphically or by a table of values.
For processing multidimensional spectra using the program VDOMUS - analogue of the program VMRIA, similar user interface. Both programs are written in programming language Pascal in Delphi 6/7 IDE and are running Windows 98-Windows 10.
The objective of the analysis of peaks. Task has 2 phases:
1.quality - determination of the number of peaks in the spectrum and their approximate centers (void);
2.quantitative - constructing the estimates of the parameters of these peaks.
Formally, the problem solution method (algorithm UPEAK) is as follows. The one-dimensional spectrum is recorded like this:
For processing multidimensional spectra using the program VDOMUS - analogue of the program VMRIA, similar user interface. Both programs are written in programming language Pascal in Delphi 6/7 IDE and are running Windows 98-Windows 10.
The objective of the analysis of peaks. Task has 2 phases:
1.quality - determination of the number of peaks in the spectrum and their approximate centers (void);
2.quantitative - constructing the estimates of the parameters of these peaks.
Formally, the problem solution method (algorithm UPEAK) is as follows. The one-dimensional spectrum is recorded like this:
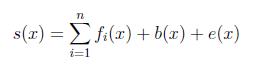
where fi is a useful component; it can be peak, or an exponent, or other function, different from zero only in a local region; b(x) is a function of the background, e(x) is the error spectrum. The variable x is usually called a channel and is measured in arbitrary integer units, x = 1, 2,
For each type of component fi, we construct a model mi(x) and mb(x). These models can be analytical functions or experimental histograms, which are parameterized in the following way:
For each type of component fi, we construct a model mi(x) and mb(x). These models can be analytical functions or experimental histograms, which are parameterized in the following way:
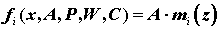
The parameters a, P, W, have a clear physical meaning:
1. A - amplitude (or area) components;
2. P - position (center) components;
3. W - half-width components;
4. C - coefficient of linear dependence of the halfwidth of the channel.
Then begins the search of peaks, which includes the following steps:
1. Spectrum provides a standard scale for the amplitude multiplied by the appropriate scalar, and the half-width of the peaks of the compression channels so that the amplitude does not exceed 1000, and the half-width of 6 channels.
2. Then carried out a smoothing of the spectrum, the construction of a low-frequency envelope from the bottom and subtract it from the spectrum.
3. Next is search the tops of the peaks on the criterion of quasi-curvature: in each point are calculated values:
and the points of local maxima of this quantity xj, provided that s(xj) > err(xj), where err(x) is the maximum error level (with accounting background) spectrum at the point x, taken for the approximate peak positions.
4.Next is the analysis of the found peaks by criteria sensitivity (sifting weak peaks) and resolution (merge is too close).
5.On the basis of the found peaks is based the estimated range of adjusted amplitude to s(x), which is then subtracted from s(x).
6.The residue is analyzed for the presence of the hidden strongest peaks, which, if discovered, are added to the list of previously found.
It then runs one or the other procedure is the analytical fit of parametric model spectrum to s(x) in the metric of least squares or robust, as a result, we obtain the estimates of the parameters A, P,W,C and their errors for each peak. Differentiation in the parameters needed to apply the methods of adjustment, is as follows:
1. A - amplitude (or area) components;
2. P - position (center) components;
3. W - half-width components;
4. C - coefficient of linear dependence of the halfwidth of the channel.
Then begins the search of peaks, which includes the following steps:
1. Spectrum provides a standard scale for the amplitude multiplied by the appropriate scalar, and the half-width of the peaks of the compression channels so that the amplitude does not exceed 1000, and the half-width of 6 channels.
2. Then carried out a smoothing of the spectrum, the construction of a low-frequency envelope from the bottom and subtract it from the spectrum.
3. Next is search the tops of the peaks on the criterion of quasi-curvature: in each point are calculated values:
and the points of local maxima of this quantity xj, provided that s(xj) > err(xj), where err(x) is the maximum error level (with accounting background) spectrum at the point x, taken for the approximate peak positions.
4.Next is the analysis of the found peaks by criteria sensitivity (sifting weak peaks) and resolution (merge is too close).
5.On the basis of the found peaks is based the estimated range of adjusted amplitude to s(x), which is then subtracted from s(x).
6.The residue is analyzed for the presence of the hidden strongest peaks, which, if discovered, are added to the list of previously found.
It then runs one or the other procedure is the analytical fit of parametric model spectrum to s(x) in the metric of least squares or robust, as a result, we obtain the estimates of the parameters A, P,W,C and their errors for each peak. Differentiation in the parameters needed to apply the methods of adjustment, is as follows:
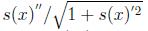
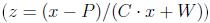
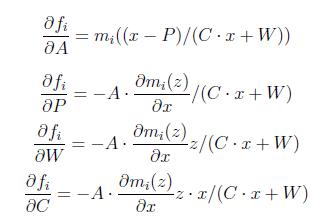
More information about the program can be found in the relevant articles of the author published on this website and in the brief reference in the program caused by pressing the button HELP.
Note that is in the testing stage, so the information and documentation concerning the program is updated periodically.
Note that is in the testing stage, so the information and documentation concerning the program is updated periodically.



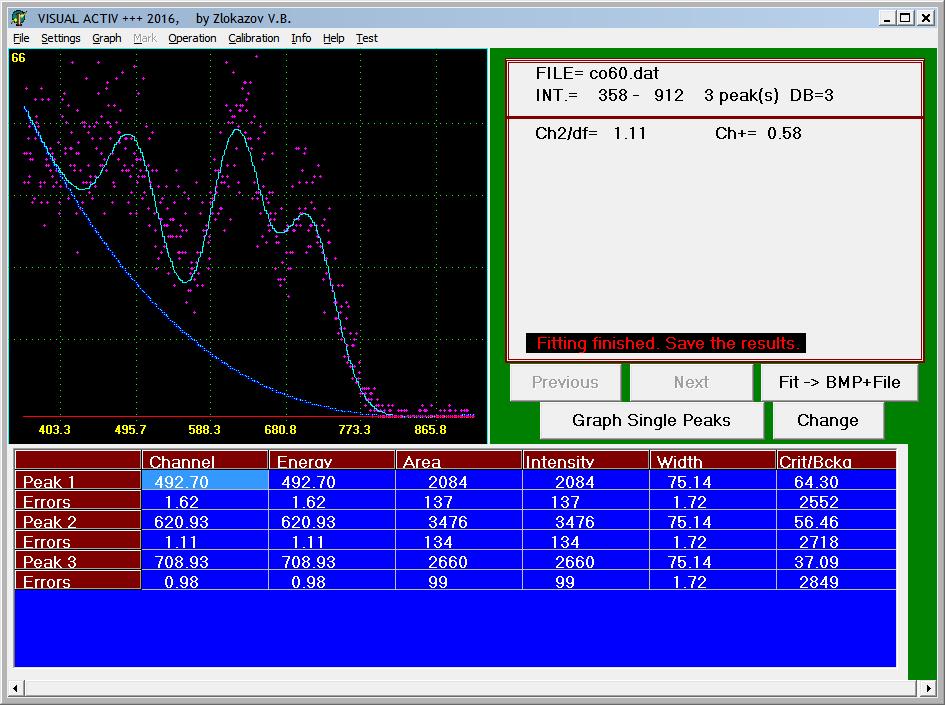
Visual Active oriented for users working with gamma-ray spectra and is essentially an offshoot of VMRIA. The mathematical apparatus VАctive does not basically differ from the above-described methods of fitting the spectra used in VMRIA. In General, methods of approximation (fitting) are fairly common in varying degrees are used in various mathematical packages and applications. Feature VActive is as automated peak find algorithm (multipic) and work with the shape of the peak. The program can work as a regular form of peak (Gaussian+background described by a polynomial of degree up to 5), and the most exotic, given, if necessary, graphically or by a table of values (the real peak).
The possibility of calibration of the spectrum, i.e., the dependency E=E(channel) energy of gamma quanta from a channel number to the Ox axis. Graduation is usually known spectra (Co-60, Cs-137) provisional definition of the positions of the centers of the peaks by the method of least squares (fitting) with the help of the program. Then you enter the analyzed spectrum of the radionuclide and specified the parameters of its peaks already in the calibrated scale.
The possibility of calibration of the spectrum, i.e., the dependency E=E(channel) energy of gamma quanta from a channel number to the Ox axis. Graduation is usually known spectra (Co-60, Cs-137) provisional definition of the positions of the centers of the peaks by the method of least squares (fitting) with the help of the program. Then you enter the analyzed spectrum of the radionuclide and specified the parameters of its peaks already in the calibrated scale.

The author of the program - Zlokazov Victor Borisovich, JINR, Dubna, Moscow Region.
Zlokazov Victor Borisovich - doctor of physico-mathematical Sciences, leading researcher, the joint Institute for nuclear research (JINR) Dubna, a member of the new York Academy of Sciences (1995 No. 45071), the International society of philosophy and cosmology (ISPC), member of editorial Board of scientific-philosophical journal "Philosophy and Cosmology".
Main stages of scientific activity.
Place of work - JINR (Dubna), mathematician, position of leading researcher. Worked as a guest scientist at Hahn-Meitner Institute (Berlin) in Germany 1991, 1992, 1994, 1995, 1996, 1997, 2005, and at the Munich FRM2 reactor of the Technical University in 2000.
Research topics - full analysis (mathematics, methods, algorithms, programs) experimental distributions of the spectra of nuclear reactions, cross sections, etc.
Research interests: the development of methods for collection and automatic analysis of experimental data and software implementation of these methods.
The total number of publications - 170.
The number of citations in international journals - 216 (2010).
The authors are open and willing to cooperate. All comments and suggestions should be sent to:
The author of the mathematical kernel: zlokazov V. B., e-mail: zlokazov@jinr.ru
Work site support: Pankov Sergey, Tula Educational Technology, JINR, Dubna:
Email: physexperiment@narod.ru
The software Department: +7-4872-58-38-35, +7-910-585-55-02
Zlokazov Victor Borisovich - doctor of physico-mathematical Sciences, leading researcher, the joint Institute for nuclear research (JINR) Dubna, a member of the new York Academy of Sciences (1995 No. 45071), the International society of philosophy and cosmology (ISPC), member of editorial Board of scientific-philosophical journal "Philosophy and Cosmology".
Main stages of scientific activity.
Place of work - JINR (Dubna), mathematician, position of leading researcher. Worked as a guest scientist at Hahn-Meitner Institute (Berlin) in Germany 1991, 1992, 1994, 1995, 1996, 1997, 2005, and at the Munich FRM2 reactor of the Technical University in 2000.
Research topics - full analysis (mathematics, methods, algorithms, programs) experimental distributions of the spectra of nuclear reactions, cross sections, etc.
Research interests: the development of methods for collection and automatic analysis of experimental data and software implementation of these methods.
The total number of publications - 170.
The number of citations in international journals - 216 (2010).
The authors are open and willing to cooperate. All comments and suggestions should be sent to:
The author of the mathematical kernel: zlokazov V. B., e-mail: zlokazov@jinr.ru
Work site support: Pankov Sergey, Tula Educational Technology, JINR, Dubna:
Email: physexperiment@narod.ru
The software Department: +7-4872-58-38-35, +7-910-585-55-02

TSD-SOFT, JINR, Tula-Dubna, 2006-2017, hy6-5@yandex.ru


















